수치 해석: 초깃값 문제
초깃값 문제
수치 해석에서 초깃값 문제 (initial value problem, IVP)란 \(\frac{dy}{dt} = f(t, y(t)), \ y(t_0) = y_0\)을 만족하는 \(y(t)\)의 근삿값을 계산하는 문제를 뜻하며, \(\frac{dy}{dt}\)로부터 \(y(t)\)를 구하는 과정을 “미분 방정식을 푼다"고 한다.
$$ \frac{d\textbf{y}}{dt} = f(t, \textbf{y}(t)), \textbf{y}(t_0) = y_0 $$함수 \(f: \mathbb{R}^{N + 1} \rightarrow \mathbb{R}^N\) (\(N > 0\)), 벡터 공간 \(\mathbb{R}^N\)의 원소 \(y_0\)과 스칼라 상수 \(t_0\)에 대하여, 아래 조건을 만족하는 \(\textbf{y}(t)\)를 미분 방정식 \(\frac{d\textbf{y}}{dt}\)에 대한 초깃값 문제라고 한다.
초깃값 문제는 독립 변수 \(t\)를 시간 (time)으로 보고, 시각 \(t = t_0\)에서의 속도가 \(y_0\)인 물체의 위치 \(y(t)\)가 시간에 따라 어떻게 변하는지를 관찰하는 문제로 볼 수도 있다.
$$ \frac{dy}{dt} = v(t), \ y(t_0) = y_0 $$피카르–린델뢰프 정리
$$ |f(x_1) - f(x_2)| \le \mathcal{L}|x_1 - x_2| $$립시츠 연속성 (Lipschitz continuity): 정의역과 공역이 모두 실수 집합 \(\mathbb{R}\)에 속하는 함수 \(f: \mathbb{R} \rightarrow \mathbb{R}\)과 스칼라 상수 \(\mathcal{L}\) (Lipschitz constant)에 대해, 다음 조건을 만족하는 함수를 립시츠 연속 (Lipschitz continuous)이라고 한다.
피카르–린델뢰프 정리 (Picard–Lindelöf theorem)는 \(\frac{dy}{dt}\)가 어떤 영역에서 연속이고 립시츠 연속일 경우, 그 영역에서 \(y(t)\)가 반드시 단 하나만 존재함을 보장해준다.
$$ \frac{dy}{dt} = f(t, y(t)), \ y(t_0) = y_0 $$피카르–린델뢰프 정리: 함수 \(f(t, y(t))\)가 직사각형 영역 \(R = \{ (t, y) \ | \ a < t < b,\) \(\ c < y < d \}\)에서 연속이고 \(y\)에 대한 열린 구간 \(c, d\)에서 립시츠 연속이면, \(R\)에 속하는 모든 \((t, y)\)에 대해 아래 조건을 만족하는 미분 방정식 \(\frac{dy}{dt}\)의 해는 반드시 존재하며, 그 해는 유일하다.
오일러 방법
오일러 방법 (Euler’s method)은 초깃값 문제를 풀기 위한 가장 간단한 수치 해석 방법으로, \(y(t)\)에서 \(t\)가 점 \(t_k\)와 충분히 가깝다면 \(y(t)\)를 \(t = t_0\)에서의 접선으로 선형 근사할 수 있다는 사실을 이용한다.
$$ y(t) \approx y(t_0) + f(t_0, y(t_0)) (t - t_0) $$여기서 \(t - t_0 = h\)라고 하면,
$$ y(t_0 + h) \approx y(t_0) + hf(t_0, y(t_0)) $$위 방정식을 일반화하여, \(t_{n + 1} = t_n + h\)라고 하면
$$ y(t_{n + 1}) \approx y(t_n) + hf(t_n, y(t_n)) $$따라서 \(y_n = y(t_n)\)일 때 다음 공식을 얻을 수 있다.
$$ y_{n + 1} \approx y_n + hf(t_n, y_n) $$\(\textbf{Algorithm 1: } \text{Euler's method}\)
\(\textbf{Require: } t_0 \text{ (Initial Point)}\)
\(\textbf{Require: } y_0 \text{ (Initial Value)}\)
\(\textbf{Require: } N \text{ (Iteration Count)}\)
\(\textbf{Require: } h \text{ (Step Size)}\)
\(\textbf{Require: } f(t, y(t))\)\(i \leftarrow 0\)
\(t_k \leftarrow t_0\)
\(y_k \leftarrow y_0\)\(\textbf{while} \ i < N \ \textbf{do}\)
\(\ \ \ \ \ \ \ \ y_k \leftarrow y_k + h \cdot f(t_k, y_k)\)
\(\ \ \ \ \ \ \ \ t_k \leftarrow t_k + h\)
\(\textbf{end while}\)
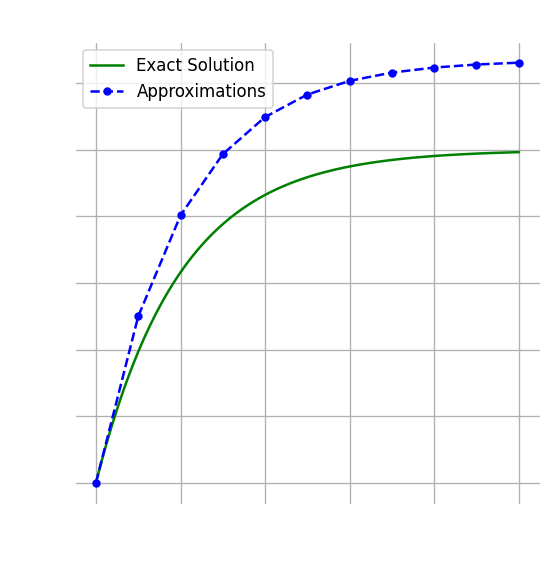
테일러 정리를 이용한 유도
오일러 방법은 테일러 정리를 통해서도 유도할 수 있다.
$$ y(b) \approx y(a) + y'(a)(b - a) + $$$$ \frac{y''(a)}{2!}(b - a)^2 $$\(a\), \(b\)와 \(\theta\)를 각각 \(a = t\), \(b = t + h\), 그리고 \(\theta \in [a, b]\)라 하면
$$ y(t + h) \approx y(t) + hy'(t) + \frac{1}{2}h^2 y''(\theta) $$\(t = t_0\), \(t_{n + 1} = t_n + h\), \(y_n = y(t_n)\)으로 놓고 나머지 항 \(\frac{1}{2}h^2 y''(\theta)\)을 생략하면 오일러 방법에 해당하는 공식을 얻을 수 있다.
$$ y_{n + 1} \approx y_n + hf(t_n, y_n) $$이때 공식 유도를 위해 생략한 나머지 항을 오일러 방법의 잔차 (residual) \(R(t, h)\)라고 한다.
$$ R(t, h) = \frac{1}{2}h^2 y''(\theta) $$또한, 오일러 방법에서 잔차로 인해 발생하는 미분 방정식의 실제 해 사이의 오차를 절단 오차 (truncation error)라고 하며, \(\mathcal{r}(t, h)\)로 나타낸다.
$$ \mathcal{r}(t, h) = \frac{1}{h} R(t, h) $$오일러 방법의 변형
초깃값 문제에서 주어지는 \(\frac{dy}{dt}\)의 정의를 이용하면 새로운 공식을 유도할 수 있다.
$$ \frac{dy}{dt} = y'(t) = f(t, y(t)) $$$$ = \lim_{h \rightarrow 0} \frac{y(t + h) - y(t)}{h} $$\(y'(t)\)를 테일러 다항식으로 나타낸 후 그대로 정리하면, 오일러 방법에 해당하는 공식을 얻을 수 있다.
$$ \frac{y(t + h) - y(t)}{h} $$$$ \approx y'(t) + \frac{1}{2}h^2 y''(\theta) $$그런데 \(y'(t) \approx \frac{y(t) - y(t - h)}{h}\)로 정의하면
$$ \frac{y(t) - y(t - h)}{h} $$$$ \approx y'(t) + \frac{1}{2}h^2 y''(\theta) $$역 오일러 방법 (backward Euler method)에 해당하는 공식을 얻는다.
$$ y_{n + 1} \approx y_n + hf(t_{n + 1}, y_{n + 1}) $$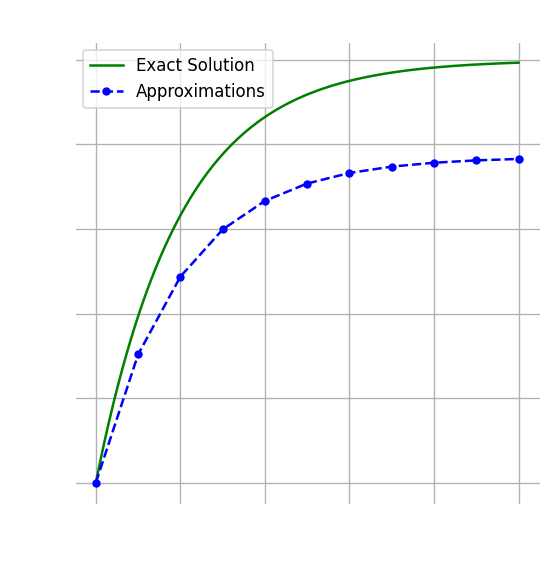
또한, \(y'(t) \approx \frac{y(t + h) - y(t - h)}{2h}\)로 정의하면
$$ \frac{y(t + h) - y(t - h)}{2h} \approx y'(t) + \frac{1}{6}h^2 y'''(\theta) $$중간점 방법 (midpoint method)에 해당하는 공식을 유도할 수 있다.
$$ y_{n + 1} \approx y_{n - 1} + 2hf(t_n, y_n) $$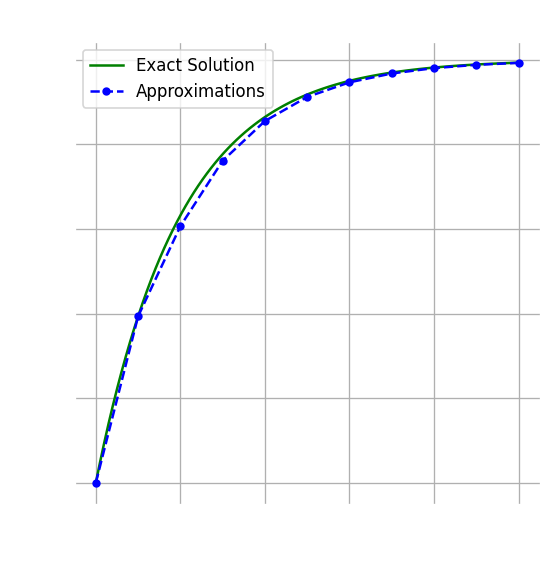
오차 분석
(추가 예정)