수학에서 최적화 (optimization)란 함수 \(f(x_1, x_2, \cdots, x_n)\)의 최댓값 또는 최솟값을 찾는 과정을 뜻한다. 기계 학습 (machine learning)에서는 극값을 찾고자 하는 함수 \(f\)를 주로 목적 함수 (objective function, criterion)이라고 하며, 극솟값만을 찾는 경우 \(f\)를 손실 함수 (loss function, cost function)이라고 하기도 한다.

\(argmax\)와 \(argmin\)

\(argmax \ f(x)\)와 \(argmin \ f(x)\)는 각각 \(f(x)\)를 최댓값 또는 최솟값으로 만드는 \(x\)를 가리킨다.

예를 들면, \(f(x) = (x - 1)^2\)는 \(x = 1\)일 때 최솟값 \(f(1)\)을 가지므로, \(argmax \ f(x) = 1\)이다.

다변수 미적분학

테일러 정리 (Taylor’s theorem)에 의하면, \(f\), \(f'\)와 \(f''\)가 모두 연속이고 미분 가능하면 \(f(\alpha)\)를 다음과 같이 \(2\)계 테일러 다항식 (Taylor polynomial of order \(2\))으로 근사하여 나타낼 수 있다.

\(\alpha - \alpha_0 = \Delta x\)라고 하면, \(\alpha = \alpha_0 + \Delta x\)인데, 이 식을 \(2\)계 테일러 다항식에 대입하면

마지막으로, \(\alpha_0\)에 \(x\)를 대입하면 \(f(x + \Delta x)\)에 대한 \(2\)계 테일러 다항식을 얻는다.

\(n\)-변수 함수 \(f(x) = f(x_1, \cdots, f_n)\)에 대한 테일러 다항식도 같은 방법으로 유도할 수 있는데, 여기서 \(\nabla f\)는 \(f\)의 기울기 벡터 (gradient)를 열 벡터 형태 (\(\begin{bmatrix} \frac{\partial f}{\partial x_1} & \cdots & \frac{\partial f}{\partial x_n}\end{bmatrix}^T\))로 나타낸 것이고, \(H_f\)는 \(f\)의 헤시안 행렬 (Hessian matrix)이다.

마지막으로, \(m\)개의 다변수 함수로 정의되는 벡터 함수 \(f = (f_1, \cdots, f_m)\)과 \(n\)개의 변수 \(x_1, \cdots, x_n\)에 대한 \(f\)의 근사식은 다음과 같다.

여기서 \(J(x)\)는 함수 \(f_1, \cdots, f_m\)에 대한 기울기 벡터 \(\nabla f_1, \cdots, \nabla f_n\)를 모두 포함하는 행렬로, 야코비 행렬 (Jacobian matrix)라고 한다.

볼록 함수

\(f(x) = f(x_1, \cdots, x_n)\)의 최적화 문제를 풀기 위해서는 볼록 함수 (convex function)라는 개념을 알아야 한다.

벡터 공간 \(K\)의 두 원소 \(x\), \(y\)와 \(0 \ge \lambda \ge 1\)가 \(\lambda x + (1 - \lambda) y \in K\)를 만족하면, \(K\)를 볼록 집합 (convex set)이라고 한다.

볼록 집합의 정의를 통해 알 수 있는 것은 두 점 \(x\)와 \(y\)가 볼록 집합의 원소라면 \(x\)와 \(y\)를 잇는 모든 선분에 속하는 원소도 볼록 집합에 포함된다는 것이다.

함수 \(f\)의 두 점 \(x\), \(y\)와 \(0 \ge \lambda \ge 1\)에 대해, 아래 조건을 만족하는 \(f\)를 볼록 함수라고 한다.

또한, 아래 조건을 만족하는 \(f\)를 엄격한 볼록 함수 (strictly convex function)이라고 한다.

\(f\)가 볼록 함수가 되려면, \(f\) 위의 두 점 \(x\)와 \(y\)를 잇는 할선 (secant)이 항상 \(f\)의 그래프 위에 있어야 한다는 것이다. 따라서 \(y = x^2\)는 볼록 함수이지만 \(y = -x^2\)는 볼록 함수가 아니다.

엄격한 볼록 함수 \(f\)의 정의역 \(x\)가 볼록 집합 \(K\)의 원소일 때, \(f\)는 단 하나의 최솟값을 가진다.

\(L^p\) 노름

벡터, 행렬이나 함수의 크기를 측정하는 방법을 노름 (norm)이라고 한다. 벡터의 노름은 주로 길이 (length) \(|v| = \sqrt{v \cdot v} = \sqrt{{v_1}^2 + {v_2}^2 + \dots}\)를 통해 정의되는데, 벡터의 길이 외에도 벡터의 크기를 나타낼 수 있는 다른 방법이 존재한다.

벡터 \(x\)의 \(L^1\) 노름 \(\| \mathbf{x} \|_1 = \sum_{i=1}^{n} |x_i|\)이다.

벡터 \(x\)의 \(L^2\) 노름 \(\| \mathbf{x} \|_2 = \sqrt{(\sum_{i=1}^{n} (x_i)^2)}\)이다.

벡터 \(x\)의 \(L^\infty\) 노름 \(\| \mathbf{x} \|_\infty = max(|x_1|, |x_2|)\)이다.

뉴턴–랩슨 방법

뉴턴–랩슨 방법 (Newton–Raphson method)은 방정식 \(f(\mathbf{x}) = 0\)의 해를 구하거나 함수 \(f(\mathbf{x})\)의 최솟값을 찾기 위해 사용할 수 있는 대표적인 방법 중 하나로, \(f(\mathbf{x})\)가 \(\mathbf{x^*} = argmin \ f(\mathbf{x})\)에서 최솟값을 가지면 \(\nabla f(\mathbf{x}) = \mathbf{0}\)임을 이용한다.

먼저, \(f(\mathbf{x})\)에서 \(argmin \ f(\mathbf{x})\)과 충분히 가까운 한 점 \(\mathbf{x_0}\)을 임의로 선택한 다음, \(\mathbf{x_{k + 1}}\)를 \(\mathbf{x_{k}}\)보다 \(\mathbf{x^*}\)에 더 가까운 점이라고 하자. \(\mathbf{x_{k + 1}}\)이 \(argmin \ f(x)\)에 가까워진다는 것은 \(\mathbf{x_{k + 1}}\)에서의 기울기 벡터 \(\nabla f(\mathbf{x_{k + 1}})\)이 \(\mathbf{0}\)에 가까워진다는 것을 뜻한다.

점 \(\mathbf{x} = \mathbf{x_{k}}\)에서 \(\nabla f(x)\)를 선형 근사식 (linear approximation) \(L(\mathbf{x})\)로 표현하면

\(L(\mathbf{x})\)에 \(\mathbf{x} = \mathbf{x_{k + 1}}\)을 대입하면

이제 \(\mathbf{x_{k}}\)가 \(\mathbf{x^*}\)와 충분히 가까워서 \(\nabla f(\mathbf{x_{k + 1}}) = \mathbf{0}\)이라고 하면

따라서 아래 방정식을 통해 \(\mathbf{x_{k + 1}}\)를 구할 수 있으며, 이때 \(\mathbf{x_{k + 1}}\)까지의 이동 거리 \(\Delta \mathbf{x} = \mathbf{x_{k + 1}} - \mathbf{x_k}\)를 스텝 크기 (step size)라고 한다.

뉴턴–랩슨 방법을 통해 \(f(x) = x^3 - 3x + 1\)의 최솟값을 찾아 보자.

1. \(x_0 = \frac{1}{2}\)

2. \(x_1 = \frac{5}{4}\)

이 과정을 계속 반복할수록 \(x_k\)가 \(x = 1\)에 점점 가까워지는 것을 확인할 수 있다.

함수 \(f(\mathbf{x})\), \(f(\mathbf{x})\)의 기울기 벡터 \(\nabla f(x)\)와 \(f(\mathbf{x})\)의 헤시안 행렬 \(H_f(x)\)가 모두 연속이고 \(\mathbf{x_0}\)이 \(\mathbf{x^*} = argmin \ f(\mathbf{x})\)에 충분히 가까우면, 뉴턴–랩슨 방법은 반드시 수렴한다.

경사 하강법

뉴턴–랩슨 방법을 이용하여 다변수 함수 \(f(\mathbf{x})\)를 최적화하기 위해서는 \(\nabla f(\mathbf{x})\)와 \(H_f(\mathbf{x})\)를 구해야 하는데, 독립 변수의 개수가 많아질수록 \(H_f(x)\)의 크기 (\(2\)-계 편도함수의 개수)가 기하급수적으로 증가한다는 단점이 존재한다.

\(f(\mathbf{x})\)가 \(n\)개의 독립 변수를 가진 다변수 함수 \(f(x_1, x_2, \cdots, x_n)\)일 때, \(\nabla f(\mathbf{x})\)와 \(H_f(\mathbf{x})\)의 크기는 각각 \(n \times 1\)과 \(n \times n\)이다. 그런데 \(H_f(\mathbf{x})\)가 대칭 행렬이므로 주대각 성분의 아랫 부분에 대한 계산을 생략하더라도 \(\frac{n(n + 1)}{2}\)번의 계산이 필요하다. \(n\)이 \(20\) 정도로 작더라도 무려 \(210\)번의 계산이 필요한 것이다.

따라서 기계 학습 (machine learning)이나 딥 러닝 (deep learning) 분야에서는 뉴턴–랩슨 방법에 비해 수렴 속도가 느리더라도 헤시안 행렬 없이 \(f(\mathbf{x})\)의 최솟값을 찾을 수 있는 경사 하강법 (gradient descent)을 주로 사용한다.

경사 하강법: 다변수 함수 \(f(\mathbf{x})\) 위의 점 \(\mathbf{x_{k}}\)이 \(argmin \ f(\mathbf{x})\)과 충분히 가깝다고 할 때, \(\mathbf{x_{k}}\)보다 \(argmin \ f(\mathbf{x})\)에 더 가까운 \(\mathbf{x_{k + 1}}\)은 아래와 같이 구할 수 있다. (단, \(\eta\) (eta)는 스칼라 상수)

방향 미분계수의 정의를 잘 생각해보면, \(\mathbf{x_{k}}\)에서 \(f(\mathbf{x})\)가 가장 빠르게 감소하는 방향 또는 최솟값으로 가장 빠르게 갈 수 있는 방향은 \(\nabla f\) 방향이라는 것을 쉽게 알 수 있다.

경사 하강법의 수렴 속도

경사 하강법처럼 함수의 최솟값을 찾을 때 \(1\)-계 도함수 또는 \(\nabla f(\mathbf{x})\)만을 사용하는 방법을 \(1\)-계 최적화 방법 (first-order optimization algorithm)이라 하며, 뉴턴–랩슨 방법처럼 \(2\)-계 도함수 또는 \(H_f(\mathbf{x})\)까지 사용하는 방법을 \(2\)-계 최적화 방법 (first-order optimization algorithm)이라고 한다.

\(1\)-계 최적화 방법이 가지는 단점에 대해 알아보기 위해, 경사 하강법으로 함수 \(f(x, y) = \frac{1}{2}(x^2 + \frac{1}{10}y^2)\)의 최솟값을 찾아보자. 이 함수는 \(x\)축 방향에서 기울기가 급격히 감소하지만, \(y\)축 방향에서는 기울기가 매우 완만하게 감소하는 낙하산 (…?) 형태를 띠고 있다.

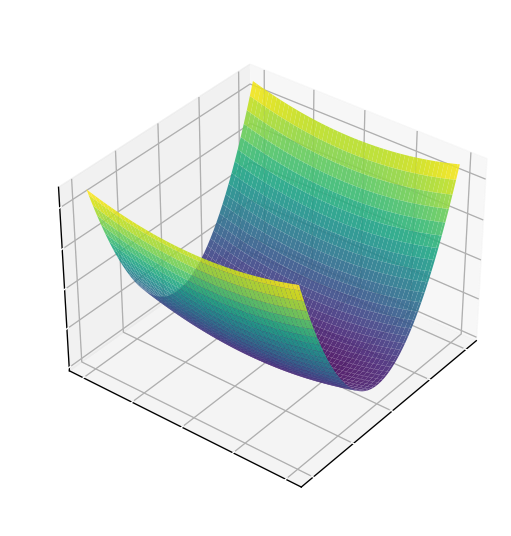
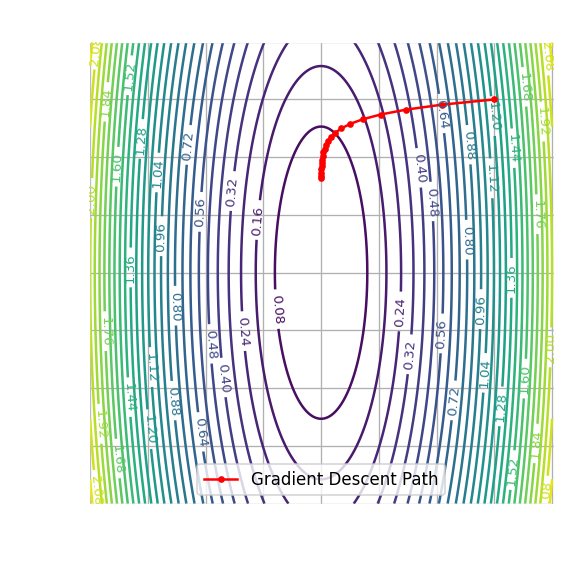
경사 하강법으로 최솟값을 구해 나가는 과정을 등고선 그래프 (contour plot)로 나타내면 \(x\)가 \(0\)에 가까워질수록 수렴 속도가 급격하게 느려지는 것을 확인할 수 있는데, 이러한 상황이 발생하는 이유는 경사 하강법이 뉴턴–랩슨 방법처럼 함수의 곡률 (curvature)을 고려하지 않고 현재 지점에서의 기울기만을 고려하기 때문이다.

대칭 행렬 \(S\)의 가장 큰 고유값 \(\lambda_{max}\)와 가장 작은 고유값 \(\lambda_{min}\)에 대해 \(\frac{|\lambda_{max}|}{|\lambda_{min}|}\)를 \(S\)의 조건수 (condition number)라고 한다.

경사 하강법의 수렴 속도가 급격히 느려지는 경우를 좀 더 자세히 설명하면, 함수 \(f(\mathbf{x})\)의 헤시안 행렬 \(H_f(\mathbf{x})\)의 조건수가 크다는 것은 \(f(\mathbf{x})\)의 한쪽 방향에서의 편도함수가 매우 급격하게 증가하고, 다른 쪽 방향에서의 편도함수는 매우 서서히 증가한다는 것을 뜻한다. 그런데 경사 하강법은 \(f(\mathbf{x})\)에 이러한 곡률 차이가 있다는 사실을 모르기 때문에, 최솟값이 있는 방향으로 이동하는 대신 현재 지점에서 기울기가 가장 가파르게 내려가는 방향으로만 움직이게 된다.

경사 하강법의 수렴 가능성

볼록 함수 \(f(\mathbf{x})\)에 대해 \(\nabla f(\mathbf{x})\)가 립시츠 연속성 (Lipschitz continuity)을 만족하면, 경사 하강법은 반드시 수렴한다.

립시츠 연속성: 정의역과 공역이 모두 실수 집합 \(\mathbb{R}\)에 속하는 함수 \(f: \mathbb{R} \rightarrow \mathbb{R}\)과 스칼라 상수 \(\mathcal{L}\) (Lipschitz constant)에 대해, 다음 조건을 만족하는 함수를 립시츠 연속 (Lipschitz continuous)이라고 한다.

참고 문헌

• G. B. Thomas, Jr., J. R. Hass, C. E. Heil, M. D. Weir, “Thomas’ Calculus,” 14th ed. Pearson Education, 2021.
• G. Strang, “Linear Algebra and Learning from Data,” Wellesley-Cambridge Press, 2019.