다변수 함수

다변수 함수 (multivariable function)는 정의역 (domain)과 치역 (range)이 모두 실수인 \(1\)-변수 함수와 달리, 정의역이 \(n \ (n > 1)\)개 실수의 순서쌍이고 치역이 실수인 함수이다.

\(n\)개 실수의 순서쌍 \((x_1, x_2, \cdots, x_n)\)들의 집합 \(D\)를 정의역으로 가지는 다변수 함수 \(f\)는 정의역의 모든 원소를 단 하나의 실수 \(w = f(x_1, x_2, \cdots, f_n)\)에 대응시키는 규칙이다.

이때, \(x_1, x_2, \cdots, x_n\)을 \(f\)의 독립 변수 (independent variable, input variable)이라고 하며, \(w\)를 \(f\)의 종속 변수 (dependent variable, output variable)라고 한다.

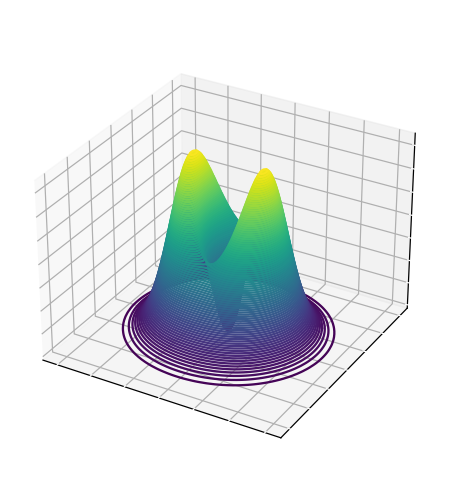
유계 영역

실수 집합에 대한 구간과 마찬가지로, \(2\)-변수 함수가 나타내는 영역은 열린 영역 (open region)일 수도 있고 닫힌 영역 (closed region)일 수도 있다.

평면 상에서 영역 \(R\)의 한 점 \(P(x_0, y_0)\)이 \(R\)에 완전히 포함되는 원판의 중심이 될 수 있을 때, \(P\)를 영역 \(R\)의 내부 점 (interior point)이라고 하며, \(P\)를 중심으로 하는 원판이 영역 \(R\)의 내부 점과 외부에 있는 점까지 포함할 경우 \(P\)를 경계 점 (boundary point)라고 한다.

내부 점과 경계 점의 개념은 단위 원판 (unit disk) \(x^2 + y^2 < 1\)과 \(x^2 + y^2 \le 1\)이 나타내는 부등식 영역을 통해 쉽게 이해할 수 있다. \(x^2 + y^2 < 1\)은 내부 점으로만 이루어진 열린 영역을 나타내고, \(x^2 + y^2 \le 1\)은 내부 점과 경계 점을 모두 포함하는 닫힌 영역을 나타낸다.

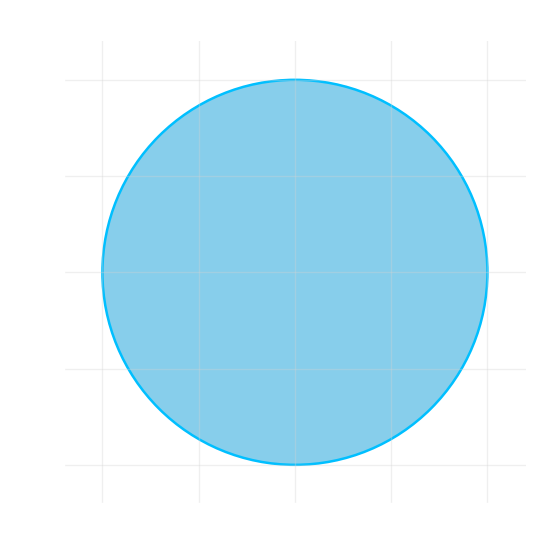
평면 상에서 유한한 반지름을 가지는 원판 안에 포함되는 영역을 유계 영역 (bounded region)이라고 한다.

예를 들면, 선분, 다각형, 원 등은 유계 영역이지만 직선, 평면, 좌표축이나 무한 구간에서 정의된 함수의 그래프는 유계 영역이 아니다.

극한과 연속

\(2\)-변수 함수의 극한을 이해할 때 주의할 점은, 독립 변수가 단 하나인 \(1\)-변수 함수에서의 극한의 정의와 달리 \((x, y)\)가 주어진 점에 접근할 때 왼쪽 방향과 오른쪽 방향 외에도 모든 방향에서 접근할 수 있다는 것이다. 이 부분을 제외한 나머지 내용은 \(1\)-변수 함수에 대한 엡실론-델타 논법 (epsilon-delta argument)과 동일하다.

“\(f(x, y)\)와 극한값 \(L\) 사이의 거리 \(|f(x, y) - L|\)를 \(\epsilon\) 미만으로 줄일 수 있니? \(\rightarrow\) \((x, y)\)와 점 \((x_0, y_0)\) 사이의 거리 \(\sqrt{(x - x_0)^2 + (y - y_0)^2}\)가 \(\delta\)로 충분히 작으면 된다!”

엡실론-델타 논법 (\(2\)-변수 함수): 함수 \(f\)에 정의역에 속하는 임의의 점 \((x, y)\)와 실수 \(\epsilon \ (\epsilon > 0)\)에 대하여, 아래 조건을 만족하는 \(\delta \ (\delta > 0)\)이 존재한다면 \((x, y)\)가 \((x_0, y_0)\)에 접근할 때 \(f\)의 극한은 \(L\)에 접근한다고 한다.

\((x, y)\)가 \((x_0, y_0)\)에 접근할 때 \(f\)의 극한은 \(L\)이라면, 다음과 같이 표현한다.

\(2\)-변수 함수의 극한을 정의하였으므로 이제 연속성을 정의한다.

함수 \(f(x, y)\)가 점 \((x_0, y_0)\)에서 정의되고, \((x, y)\)가 \((x_0, y_0)\)에 접근할 때 \(f\)의 극한 \(L = f(x_0, y_0)\)일 때, \(f(x, y)\)는 점 \((x_0, y_0)\)에서 연속이다.

편도함수

점 \((x_0, y_0)\)에서 \(x\)에 대한 함수 \(f(x, y)\)의 편미분계수 (partial derivative)는 극한이 존재할 경우 다음과 같다.

또한, 점 \((x_0, y_0)\)에서 \(y\)에 대한 함수 \(f(x, y)\)의 편미분계수는 극한이 존재할 경우 다음과 같다.

점 \((x_0, y_0)\)에서 \(x\)에 대한 함수 \(f(x, y)\)의 편미분계수는 \(x = x_0\)에서 \(x\)에 대한 \(1\)-변수 함수 \(f(x, y_0)\)의 미분계수와 같다. 마찬가지로, 점 \((x_0, y_0)\)에서 \(y\)에 대한 함수 \(f(x, y)\)의 편미분계수는 \(y = x_0\)에서 \(y\)에 대한 \(1\)-변수 함수 \(f(x_0, y)\)의 미분계수와 같다. 편미분계수와 미분계수의 구별을 위해, 편미분계수는 미분계수의 \(d\) 대신 \(\partial\) (partial, round(-ed d))기호를 사용한다.

편미분계수가 존재하는 모든 점들의 집합을 정의역으로 하는 편도함수는 다변수 함수의 독립 변수 중에 하나를 선택하고 나머지 변수들은 상수 취급하여 계산한, 단 하나의 독립 변수에 대한 도함수를 뜻하며, 보통 \(\frac{\partial f}{\partial x}\), \(\frac{\partial z}{\partial x}\), 또는 \(f_x\)와 같이 나타낸다.

클레로의 정리

함수 \(f(x, y)\)를 두 번 미분하면 \(2\)계 편도함수를 얻을 수 있다. 예를 들면, \(f\)를 \(y\)에 대해 먼저 미분하고 다시 \(x\)에 대해 미분하여 얻은 \(2\)계 편도함수는 아래와 같이 나타낸다.

\(2\)계 편도함수 \(\frac{\partial^2 f}{\partial x \partial y}\)와 \(\frac{\partial^2 f}{\partial y \partial x}\)가 항상 같은 것은 아닌데, 아래 정리에 의하면 두 \(2\)계 편도함수가 같기 위해서는 \(f\), \(f_x\), \(f_y\), \(f_{xy}\)와 \(f_{yx}\)가 모두 연속이어야 한다.

클레로의 정리 (Clairaut’s theorem): 함수 \(f\)와 도함수 \(f_x\), \(f_y\), \(f_{xy}\)와 \(f_{yx}\)가 점 \((a, b)\)를 포함하는 열린 영역에서 정의되고 \((a, b)\)에서 모두 연속이면 다음이 성립한다.

미분 가능성

함수 \(z = f(x, y)\)에서 \(f_x(x_0, y_0)\)과 \(f_y(x_0, y_0)\)이 존재하고 \(\Delta z\)가 아래 방정식을 만족하면, \(f\)는 \((x_0, y_0)\)에서 미분 가능하다. (단, \(\Delta x \rightarrow 0\)이고 \(\Delta y \rightarrow 0\)일 때 \(\epsilon_1 \rightarrow 0\)이고 \(\epsilon_2 \rightarrow 0\))

연쇄 법칙

\(1\)-변수 함수 \(y = f(u)\)와 \(u = g(x)\)로 이루어진 합성 함수 \(f \circ g\)의 도함수 \((f \circ g)'\)는 아래와 같이 연쇄 법칙 (chain rule)을 이용하여 구할 수 있는데, 여기서 \(u\)는 중간 변수 (intermediate variable)이고 \(x\)는 독립 변수이다.

합성 함수가 여러 개의 중간 변수와 독립 변수를 가지더라도, 연쇄 법칙을 이용하면 (편)도함수를 쉽게 계산할 수 있다. 예를 들어, 독립 변수 \(t\)와 중간 변수 \(x = x(t)\), \(y = y(t)\)로 이루어진 합성 함수의 도함수를 구해보자.

\(2\)-변수 함수 \(w = f(x, y)\)가 미분 가능하고 \(t\)에 대한 두 함수 \(x = x(t)\), \(y = y(t)\)가 미분 가능할 때, \(w = f(x(t), y(t))\)의 도함수는 다음과 같다.

중간 변수가 \(x = x(t)\), \(y = y(t)\), \(z = z(t)\)로 하나 더 늘어나더라도, \(z\)에 대한 항을 하나만 더 추가해주면 하나의 독립 변수 \(t\)와 세 중간 변수 \(x\), \(y\)와 \(z\)에 대한 공식을 얻을 수 있다.

독립 변수의 개수가 하나 더 늘어나면 공식은 어떻게 바뀔까? 두 독립 변수 \(r\), \(s\)와 세 중간 변수 \(x = g(r, s)\), \(y = h(r, s)\), \(z = k(r, s)\)로 이루어진 함수 \(w = f(x, y, z)\)의 편도함수 \(\frac{dw}{dr}\)와 \(\frac{dw}{ds}\)는 아래와 같이 구할 수 있다.

일반적으로, 여러 개의 중간 변수와 독립 변수를 가지는 합성 함수 \(w = f(x, y, \cdots)\)의 \(p\)에 대한 (편)도함수는 각각의 중간 변수에 대한 \(w\)의 편도함수로 이루어진 벡터 \((\frac{\partial w}{\partial x}, \frac{\partial w}{\partial y}, \cdots)\)와 독립 변수 \(p\)에 대한 중간 변수의 편도함수로 이루어진 벡터 \((\frac{\partial x}{\partial p}, \frac{\partial y}{\partial p}, \cdots)\)의 내적으로 볼 수 있다.

방향 도함수

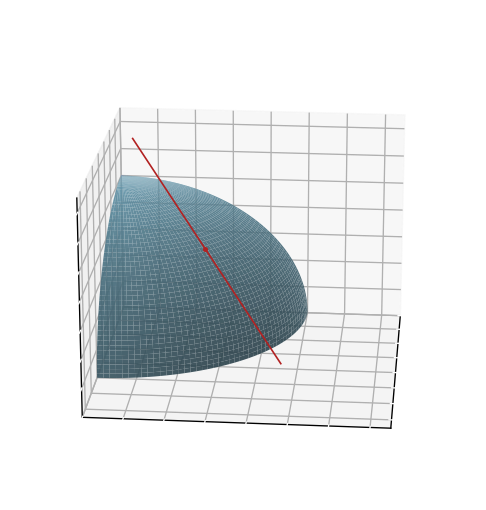
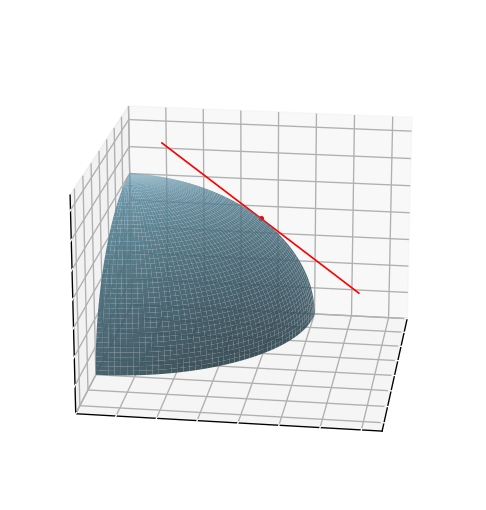
점 \(P(x_0, y_0)\)에서 함수 \(z = f(x, y)\)의 편미분계수는 \(P\)에서 \(x\)값 또는 \(y\)값이 변화함에 따라 \(z\)가 어떻게 변화하는지를 나타내는 순간변화율이자, \(P\)를 지나고 \(x\)축 또는 \(y\)축과 평행한 접선의 기울기를 나타낸다.

이제 \(x\)축 또는 \(y\)축과 평행한 방향 대신, 임의의 벡터 \(u\)의 방향으로 \(P\)을 지날 때의 \(u\) 방향에 대한 \(z\)의 변화율을 생각해보자. 단위 벡터 \(u = u_1 i + u_2 j = (u_1, u_2)\)일 때 \(x = x_0 + su_1\)이고 \(y = y_0 + su_2\)라고 하면, \(x\)와 \(y\)는 \(P\)를 지나고 \(u\) 방향으로 향하는 직선의 방정식이다.

단위 벡터 \(u = u_1 i + u_2 j\) 방향에 대한 \(P(x_0, y_0)\)에서의 \(f\)의 방향 미분계수 (directional derivative)는 극한이 존재하면 다음과 같이 정의된다.

일반적으로, \(u\) 방향에 대한 \(P\)에서의 \(f\)의 방향 미분계수는 \(D_u f(P_0)\)과 같이 나타낸다.

기울기 벡터

연쇄 법칙을 이용하면 \(f\)의 방향 미분계수를 쉽게 구할 수 있다.

따라서 \(u\) 방향에 대한 \(P\)에서의 \(f\)의 방향 미분계수는 벡터 \(f_x(x_0, y_0) i + f_y(x_0, y_0) j\)와 \(u\)의 내적 \(\nabla f \cdot u\)이다.

다음과 같은 벡터를 \(f(x, y)\)의 기울기 벡터 (gradient vector, gradient) \(\nabla f\) (grad \(f\), del \(f\))라고 한다.

기울기 벡터를 이용해 \(u = \frac{i}{\sqrt{2}} + \frac{j}{\sqrt{2}}\) 방향에 대한 \(P(1, 1)\)에서의 함수 \(f(x, y) = \frac{x^2}{2} + \frac{y^2}{2}\)의 방향 미분 계수를 계산해보자.

방향 미분계수의 성질

\(u\) 방향에 대한 \(P\)에서의 \(f\)의 방향 미분계수 \(D_u f\)는 \(\nabla f \cdot u\)라고 하였는데, \(u\)가 단위 벡터이므로 \(\nabla f \cdot u = |\nabla f| \ cos \ \theta\)가 된다. 따라서 두 벡터 \(\nabla f\)와 \(u\) 사이의 각 \(\theta\)를 통해 아래와 같은 성질을 얻을 수 있다.

1. \(cos \ \theta = 1\)이라면 \(u\)는 \(\nabla f\)와 같은 방향이고 \(f\)는 가장 빠르게 증가한다.
2. \(cos \ \theta = -1\)이라면 \(u\)는 \(\nabla f\)의 반대 방향이고 \(f\)는 가장 빠르게 감소한다.
3. \(cos \ \theta = 0\)이라면 \(u\)는 \(\nabla f\)와 수직이고 \(f\)의 변화가 \(0\)이다.

등위곡선의 접선

미분 가능한 함수 \(f(x, y)\)와 매끄러운 곡선 \(r = g(t)i + h(t)j\)에 대해 \(f(g(t), h(t)) = c\)이면, \(r\)을 \(f\)의 등위 곡선 (level curve)이라고 한다.

\(f(g(t), h(t)) = c\)의 양변을 \(t\)에 대해 미분하면, \(\nabla f\)와 등위 곡선이 어떤 관계를 가지는지를 확인할 수 있다.

따라서 \(f(x, y)\)의 정의역 내의 모든 점에서의 \(\nabla f\)는 그 점을 지나는 등위 곡선에 항상 수직임을 알 수 있다.

극값과 안장점

\(1\)-변수 함수 \(f(x)\)에서는 최댓값 (absolute maximum)과 최솟값 (absolute maximum)을 아래와 같이 정의하고, 특정 구간에 대한 최댓값과 최솟값을 각각 극댓값 (local maximum)과 극솟값 (local minimum)이라고 하였다.

함수 \(f(x)\)의 정의역에 포함된 모든 점 \(x\)에 대해 \(f(x) \le f(c)\)를 만족하는 점 \(c\)를 \(f\)의 최댓값 (absolute maximum)이라고 하며, \(f(x) \ge f(c)\)를 만족하는 점 \(c\)를 \(f\)의 최솟값 (absolute maximum)이라고 한다.

이제 \(2\)-변수 함수 \(f(x, y)\)의 극댓값과 극솟값을 정의한다.

\(f(x, y)\)가 점 \((a, b)\)를 포함하는 유계 영역 \(R\)에서 정의되었다고 하자.

1. \((a, b)\)를 중심으로 하는 원판 내의 모든 점 \((x, y)\)에서 \(f(a, b) \ge f(x, y)\)이면, \(f(a, b)\)는 \(f\)의 극댓값이다.
2. \((a, b)\)를 중심으로 하는 원판 내의 모든 점 \((x, y)\)에서 \(f(a, b) \le f(x, y)\)이면, \(f(a, b)\)는 \(f\)의 극솟값이다.

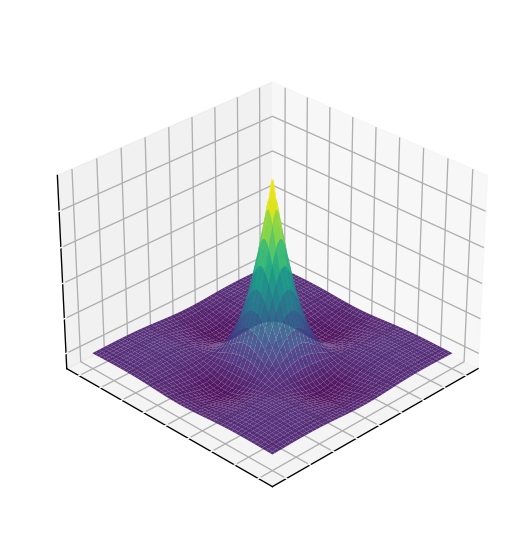
예를 들어, \((0, 0)\)을 중심으로 하고 반지름이 \(2\pi\)인 원판 \(R\)에서 정의된 \(f(x, y) = \cos x \cos y \ e^{-\sqrt{x^2 + y^2}}\)의 그래프를 보면 산의 봉우리 (peak)처럼 생긴 곳에 극댓값, 산의 골짜기 (valley)처럼 생긴 곳에 극솟값이 있다는 것을 알 수 있다.

\(f(x, y)\)가 유계 영역 \(R\)의 내부 점 \((a, b)\)에서 극값을 가지고, 이 점에서 편미분계수 \(f_x\)와 \(f_y\)가 존재하면, \(f_x(a, b) = f_y(a, b) = 0\)이다.

\(1\)-변수 함수에서는 극값을 구하기 위해 그래프에서 접선의 기울기가 \(0\)인, 수평 접선을 가지는 점을 찾았다면, \(2\)-변수 함수에서는 극값을 구하기 위해 수평 접선 대신 수평 접평면 (tangent plane)을 가지는 점을 찾아야 한다.

점 \(P(x_0, y_0, z_0)\)에서 \(f(x, y, z) = c\)에 대한 접평면의 방정식은

이므로, \(P(x_0, y_0, f(x_0, y_0))\)에서 \(z = f(x, y)\)에 대한 접평면의 방정식은

이다. 이 방정식에 \(f_x(x_0, y_0) = f_y(x_0, y_0) = 0\)을 대입하면 \(z = f(a, b)\)가 되므로, (2)-변수 함수에서 극값을 가지는 점의 접평면은 항상 수평이어야 한다는 것을 알 수 있다.

\(f(x, y)\)의 정의역에 속한 점 \(P\)에 대해 \(f_x(P) = f_y(P) = 0\)이거나 \(f_x(P)\)와 \(f_y(P)\) 중에서 하나 이상이 존재하지 않는다면, \(P\)를 \(f\)의 임계점 (critical point)라고 한다.

\(1\)-변수 함수에서는 \(f'(x)\)의 증감이 반대로 바뀌는 변곡점 (inflection point)이 존재했다면, 미분 가능한 \(2\)-변수 함수에서는 안장점 (saddle point)이라는 새로운 개념이 등장한다.

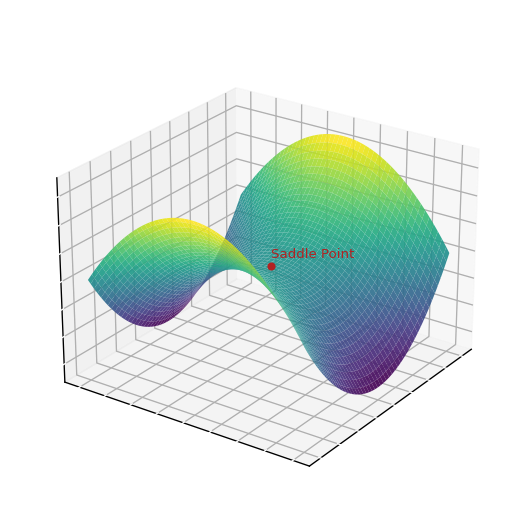
미분 가능한 함수 \(f(x, y)\)가 임계점 \((a, b)\)를 중심으로 하는 모든 열린 원판에서 \(f(x_0, y_0) > f(a, b)\)가 성립하는 점 \((x_0, y_0)\)과 \(f(x_1, y_1) < f(a, b)\)가 성립하는 또다른 점 \((x_1, y_1)\)이 동시에 존재할 때, \((a, b)\)를 안장점이라고 한다.

헤시안 행렬

다변수 함수 \(f(x_1, x_2, \cdots, x_n)\)의 모든 \(2\)-계 도함수가 포함된 \(n \times n\) 크기의 행렬을 헤시안 행렬 (Hessian matrix)이라고 하며, \(H_f\)와 같이 나타낸다.

예를 들면, \(2\)-변수 함수 \(z = f(x, y)\)의 헤시안 행렬 \(H_f\)는 다음과 같다.

클레로의 정리에 의하면, 영역 \(R\)에서 \(f\), \(f_x\), \(f_y\), \(f_{xy}\)와 \(f_{yx}\)가 모두 연속일 때 \(f_{xy} = f_{yx}\)이므로 \(H_f\)는 대칭 행렬 (symmetric matrix)이 된다. 이제 \(H_f\)를 선형 대수의 관점에서 보면, \(H_f\)는 대칭 행렬이므로 \(H_f\)의 모든 고유값은 실수 (real number)이고, 스펙트럼 정리 (spectral theorem)에 의해 \(H_f = Q \Lambda Q^T = Q \Lambda Q^{-1}\) (단, \(Q\)는 정규 직교 행렬) 형태로 분해할 수 있다.

점 \(P(a, b)\)에서 \(H_f\)의 모든 고유값이 양수라면 \(H_f\)를 양의 정부호 행렬 (positive definite matrix), \(H_f\)의 모든 고유값이 음수라면 \(H_f\)를 음의 정부호 행렬 (negative definite matrix)이라고 하는데, \(H_f\)가 양의 정부호 행렬인지 음의 정부호 행렬인지에 따라 \(f\)는 다음과 같은 특성을 가진다.

점 \(P(a, b)\)가 포함된 영역 \(R\)에서 함수 \(f\), \(f_x\), \(f_y\), \(f_{xy}\)와 \(f_{yx}\)가 모두 연속이고, \(f_x(a, b) = f_y(a, b) = 0\)이라고 가정하자.

1. \(P\)에서 \(f_{xx} < 0\)이고 \(|H_f| = f_{xx} f_{yy} - {f_{xy}}^2 > 0\)이면, \(f\)는 \(P\)에서 극댓값을 가진다.
2. \(P\)에서 \(f_{xx} > 0\)이고 \(|H_f| = f_{xx} f_{yy} - {f_{xy}}^2 > 0\)이면, \(f\)는 \(P\)에서 극솟값을 가진다.
3. \(P\)에서 \(|H_f| = f_{xx} f_{yy} - {f_{xy}}^2 < 0\)이면, \(P\)는 안장점이다.
4. \(|H_f| = f_{xx} f_{yy} - {f_{xy}}^2 = 0\)이면, \(P\)가 어떤 점인지 판정할 수 없으므로, 다른 방법으로 \(P\)를 조사해야 한다.

라그랑주 승수법

라그랑주 승수법 (method of Lagrange multipliers)은 정의역에 대한 제약 조건 (constraint)이 주어진 함수, 즉 정의역이 곡선, 원판이나 닫힌 영역 등으로 제한되어 있는 함수의 극값을 찾을 수 있는 방법을 뜻한다.

\(f(x, y, z)\)가 매끄러운 곡선 \(r(t) = x(t)i + y(t)j + z(t)k\)을 포함하는 영역에서 미분 가능하고, \(f\)가 \(r(t)\) 위의 점 \(P\)에서 극값을 가지면, \(P\)에서 \(\nabla f\)는 \(r(t)\)에 직교하고 \(\nabla f \cdot r' = 0\)이다.

\(f\)가 \(P\)에서 극값을 가진다는 것은 \(\nabla f\)가 \(P\)를 지나면서 미분 가능한 모든 곡선의 접선 벡터와 수직이라는 것을 뜻한다. 또한, \(\nabla g\)는 등위곡면 \(g = 0\)에 수직하므로 \(\nabla g\)도 \(P\)를 지나면서 미분 가능한 모든 곡선의 접선 벡터와 수직이다. 따라서 \(\nabla f\)와 \(\nabla g\)는 평행하고 적당한 스칼라 상수 \(\lambda\)에 대해 \(\nabla f = \lambda \nabla g\)로 나타낼 수 있다.

라그랑주 승수법: \(f(x, y, z)\)와 \(g(x, y, z)\)가 미분 가능한 함수이고 \(g(x, y, z) = c\)일 때 \(\nabla g \ne 0\)이라고 가정하자. 제약 조건 \(g(x, y, z) = c\)을 만족하는 \(f\)의 극댓값 또는 극솟값이 존재한다면, 다음과 같은 방정식을 해결하여 \(f\)의 극댓값 또는 극솟값을 찾을 수 있다.

이때 상수 \(\lambda\)를 라그랑주 승수 (Lagrange multiplier)라고 한다.

예를 들면, 타원 \(\frac{x^2}{8} + \frac{y^2}{2} = 1\) 위에서 함수 \(f(x, y) = xy\)의 최댓값과 최솟값을 구하는 문제를 생각해보자.

(추가 예정)

참고 문헌

• G. B. Thomas, Jr., J. R. Hass, C. E. Heil, M. D. Weir, “Thomas’ Calculus,” 14th ed. Pearson Education, 2021.
• G. Strang, “Linear Algebra and Learning from Data,” Wellesley-Cambridge Press, 2019.