선형 대수: 직교성
부분 공간 사이의 직교 관계
두 벡터 \(v\)와 \(w\)가 직교 (orthogonal) 관계에 있다는 것은 \(v\)와 \(w\)의 내적이 \(0\), 즉 \(v \cdot w = v^T w = 0\)이라는 것을 뜻한다.
벡터 공간 (부분 공간)도 벡터와 마찬가지로 직교 관계를 정의할 수 있다.
벡터 공간 \(V\)와 \(W\)에서, \(V\)의 모든 벡터 \(v\)와 \(W\)의 모든 벡터 \(w\)에 대해 \(v^T w = 0\)일 때, \(V\)와 \(W\)는 직교 관계에 있다. 이때, \(V\)와 \(W\)가 서로 만나는 지점은 영 벡터 단 하나뿐이다.
따라서 두 벡터 공간의 직교 관계는 두 평면의 수직 (perpendicular) 관계와 달리, 영 벡터 외에는 어떠한 지점도 공유하지 않는다.
이제 네 개의 주요 부분 공간에 대해 다시 생각해보자. \(Ax = b\)에서 \(N(A)\)는 \(Ax = 0\)을 만족하는 모든 \(x\)가 속한 공간이고, \(C(A^T)\)는 \(A\)의 모든 행과 \(y\)의 선형 결합 \(A^Ty\)이 속한 공간이다. 그런데 \(x^T(A^Ty) = (Ax)^Ty = 0\)이므로, \(N(A)\)와 \(C(A^T)\)는 직교 관계임을 알 수 있다. 마찬가지로 \(N(A^T)\)와 \(C(A)\)도 직교 관계에 있다.
\(N(A)\)와 \(C(A^T)\), 그리고 \(N(A^T)\)와 \(C(A)\)는 직교 관계에 있다.
직선에 대한 정사영
원점을 지나고 \(a = (a_1, a_2, \cdots, a_m)\) 방향을 향하는 직선 \(r = \mathbf{0} + ta\) (단, \(t\)는 스칼라 값)과 임의의 벡터 \(b = (b_1, b_2, \cdots, b_m)\)가 어떤 좌표계에 존재한다고 하자. \(r\) 위의 점 중에서 \(b\)와 가장 가까운 점을 지나는 벡터 \(p\)는 \(r\)에 대한 \(b\)의 정사영 (projection)을 통해 구할 수 있다.
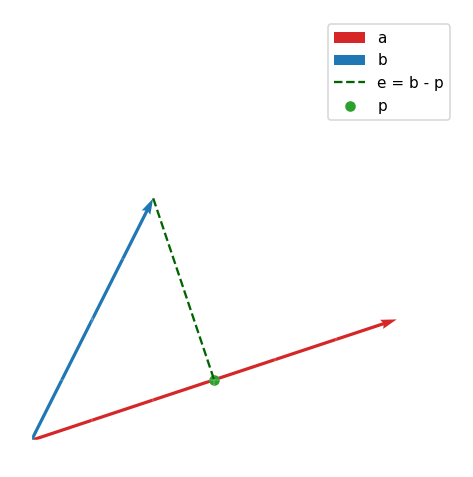
벡터 \(p\)는 \(r\) 위에 있으므로 스칼라 값 \(\hat{x}\)을 이용해 \(p = \hat{x}a\)로 나타낸다.
점선 \(e = b - p = b - \hat{x}a\)는 “오차 (error)“라고도 하며, \(e\)가 \(a\)와 수직이기 때문에 \(a \cdot e = 0\)임을 이용하면 \(\hat{x}\)의 값을 계산할 수 있다.
$$ a \cdot (b - \hat{x}a) = 0 $$$$ a \cdot b - a \cdot \hat{x}a = 0 $$$$ \therefore \hat{x} = \frac{a \cdot b}{a \cdot a} = \frac{a^T b}{a^T a} $$직선 \(r = ta\)에 대한 \(b\)의 정사영 \(p = \hat{x}a = \frac{a^T b}{a^T a}a\)이다.
\(p\)에 대한 공식에서 \(b\)를 제외한 부분을 묶어 하나의 행렬로 나타내보자.
\(p = Pb\)를 만족하는 \(P = \frac{a a^T}{a^T a}\)를 \(b\)에 대한 정사영 행렬 \(P\)라고 한다.
부분공간에 대한 정사영
직선에 대한 정사영 문제를 일반화하여, \(\mathbf{R}^m\)의 벡터 \(a_1, a_2, \cdots, a_n\)가 서로 선형 독립일 때, 이 벡터들로 만들어지는 행렬 \(A = \begin{bmatrix}a_1, a_2, \cdots, a_n\end{bmatrix}\)에 대해 \(b\)와 가장 가까운 점을 지나는 벡터 \(p = \hat{x_1}a_1 + \cdots + \hat{x_n}a_n\)와 정사영 행렬 \(P\)를 구한다고 하자.
\(n = 1\)인 경우에는 \(A = \begin{bmatrix}a_1\end{bmatrix}\)이므로 직선에 대한 정사영 문제가 되고, \(n > 1\)인 경우에는 \(n\)차원의 부분공간에 대한 정사영 문제가 된다. 이제 아래 과정을 통해 부분공간에 대한 정사영 문제를 해결해보자.
$$ A^T \cdot (b - A\hat{x}) = 0 $$$$ A^T b - A^T A\hat{x} = 0 $$$$ A^T A\hat{x} = A^T b $$$$ \hat{x} = (A^T A)^{-1} A^T b $$
- 벡터 \(\hat{x} = (\hat{x_1}, \hat{x_2}, \cdots, \hat{x_n})\)을 계산한다.
$$ p = A\hat{x} = A(A^T A)^{-1} A^T b $$
- \(\hat{x}\)를 이용해 \(p = \hat{x}A\)를 구한다.
$$ p = Pb = (A(A^T A)^{-1} A^T) b $$$$ P = A(A^T A)^{-1} A^T $$
- \(A\)에 대한 \(b\)의 정사영 행렬 \(P\)를 찾는다.
여기서 주의할 점은 \(A\)가 직사각 행렬이기 때문에 \(A\)의 역행렬 \(A^{-1}\)이 존재하지 않을 수도 있다는 것이다. 따라서 \(P\)의 \((A^T A)^{-1}\) 부분을 \(A^{-1} (A^T)^{-1}\)로 전개하지 않도록 주의하자.
\(A^T A\)가 가역 행렬이라면 \(A\)의 모든 열은 선형 독립이고, 그 역도 성립한다.
정규 직교 기저
아래 조건을 만족하는 벡터 \(q_1, q_2, \cdots, q_n\)를 정규 직교 (orthonormal) 벡터라고 한다.**
- \(i \ne j\)일 때, \({q_i}^Tq_j = 0\) (직교 벡터)
- \(i = j\)일 때, \({q_i}^Tq_j = 1\) (단위 벡터)
모든 열이 정규 직교 벡터인 직교 행렬 (orthogonal matrix) \(Q\)는 중요한 특징을 가지는데, 바로 \(Q^T Q = I\)라는 것이다. 특히, \(Q\)가 정사각 행렬일 경우 \(Q^T = Q^{-1}\)이다.
이제 정규 직교 행렬의 대표적인 예시인 회전 행렬 (rotation matrix)과 반사 행렬 (reflection matrix)에 대해 살펴보자.
$$ Q^T = Q^{-1} = \begin{bmatrix} cos \ \theta & sin \ \theta \\ -sin \ \theta & cos \ \theta \end{bmatrix} $$$$ (\because q_1 \cdot q_2 = 0 \ \text{and} \ sin^2 \ \theta + cos^2 \ \theta = 1) $$
- \(2 \times 2\) 크기의 회전 행렬 \(Q = \begin{bmatrix}cos \theta & -sin \theta \\ sin \theta & cos \theta\end{bmatrix}\)은 2차원 좌표 평면 위의 모든 벡터를 원점을 기준으로 \(\theta\)만큼 회전시킨다.
- 단위 벡터 \(u\)에 대해 \(Q = I - 2uu^T\)라고 하면 (\(uu^T\)는 \(u^Tu = |u|^2 = 1\)와 달리 행렬임에 유의), \(Q\)는 직선 \(u\)를 기준으로 점을 대칭 이동 (반사)시키는 반사 행렬이다.
그람–슈미트 과정
그람–슈미트 과정 (Gram–Schmidt process)은 선형 독립인 세 벡터 \(a\), \(b\)와 \(c\)를 직교 벡터 \(A\), \(B\)와 \(C\)로 만드는 과정을 뜻한다. 행렬 \(A\)가 직교 행렬인 경우, \(A^T A\) 형태의 수식을 \(I\)로 바꿀 수도 있고 \(A\)가 정사각 행렬일 때는 \(A\)의 역행렬 \(A^{-1} = A^T\)도 쉽게 구할 수 있기 때문에 이러한 과정은 매우 유용하다.
$$ A_0 = a $$$$ B_0 = b - \frac{A^T b}{A^T A}A $$$$ C_0 = c - \frac{A^T c}{A^T A}A - \frac{B^T c}{B^T B}B $$마지막으로 \(A_0\), \(B_0\)과 \(C_0\)을 각각 \(|A_0|\), \(|B_0|\)과 \(|C_0|\)으로 나눠준다.
$$ A = \frac{A_0}{|A_0|} $$$$ B = \frac{B_0}{|B_0|} $$$$ C = \frac{C_0}{|C_0|} $$\(A = QR\) 분해
모든 열이 선형 독립인 행렬 \(A\)에 그람–슈미트 과정을 적용하여 만들어진 \(Q\)에 대해 \(A = QR\)을 만족한다.
이때, \(R = Q^T A\)는 상삼각 행렬이다.